Главная - Трудовое право - Перенос из одной части уравнения в другую дробь

Перенос из одной части уравнения в другую дробь

Оглавление:

Основные приемы решения уравнений.
Основы алгебры/Правило переноса слагаемого
Решение линейных уравнений 7 класс
Miassats.Ru
Линейные уравнения с дробями
Линейные уравнения. Решение линейных уравнений. Правило переноса слагаемого.
Решение уравнений
Как решать дробные уравнения?
Решение уравнений с переменной в знаменателе дроби

Основные приемы решения уравнений.

Таким образом, (4) есть верное числовое равенство. Но это означает, что a есть корень уравнения (2).

Итак, каждый корень уравнения (1) является также корнем уравнения (2), т. е. (1)

(2).

Аналогично доказывается, что (2)(1).

Итак, мы доказали, что при переносе любого слагаемого из одной части уравнения в другую с противоположным знаком получается равносильное уравнение.

В частности, мы можем, если нужно, перенести все слагаемые в одну часть уравнения. Иначе говоря, f(x) = g(x) f(x) — g(x) = 0 что является частным случаем эквивалентности (1)(2). Мы видим, что любое уравнение с одним неизвестным можно заменить эквивалентным уравнением вида h(х) = 0, т. е. уравнением, в левой части которого стоит некоторая функция, а правая часть равна нулю.

Указанное преобразование (перенос членов из одной части уравнения в другую) применяется при решении уравнений чрезвычайно часто.

Основы алгебры/Правило переноса слагаемого

Но можно раскрыть скобку и получить два слагаемых: и . Такие два слагаемых уже можно переносить по отдельности.

Точно также можно преобразовывать неравенства. Например:

Перенесём все числа в одну сторону. В итоге имеем: или Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным.

По одну сторону знака «равно» оно сократится с тем, что было.

По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус». Возьмём уравнение: Допустим мы хотим перенести все иксы из левой части уравнения в правую. Вычтем из обеих частей Слева сократится с , и иксов не останется. Справа сократится с , и останется : Теперь можно привести подобные слагаемые: Теперь нужно проверить, совпадают ли левая и правая части уравнения.

Заменим неизвестную переменную получившимся результатом:

Решение линейных уравнений 7 класс

Рассмотрим другое уравнение.

5x = 4x + 9 По перенесем «4x» из левой части уравнения в правую, поменяв знак на противоположный. Несмотря на то, что перед «4x» не стоит никакого знака, мы понимаем, что перед «4x» стоит знак «+». 5x = 4x + 9 5x = +4x + 9 5x − 4x = 9 Теперь и решим уравнение до конца.

5x − 4x = 9 x = 9 Ответ: x = 9 Запомните! В любом уравнении можно разделить левую и правую часть на одно и то же число. Но нельзя делить на неизвестное!

Разберемся на примере, как использовать правило деления при решении линейных уравнений.

Число «4», которое стоит при «x», называют числовым коэффициентом при неизвестном.

Между числовым коэффициентом и неизвестном всегда стоит действие умножение.

Рекомендуем прочесть: Расписка на получение денег за гараж бланк

Miassats.Ru

То есть: Всё предельно просто.

Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент «1».

И, пожалуйста, не ищите общий знаменатель!

Не надо его здесь… Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.: Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например: В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями.

Например: Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки: Но не забывайте о порядке деления!

В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться.

Обратите внимание, например: В первом случае (выражение слева): Во втором (выражение справа): Чувствуете разницу? 4 и 1/9! А чем задается порядок деления?

Или скобками, или (как здесь) длиной горизонтальных черточек.

Линейные уравнения с дробями

Найдем дополнительный множитель к каждой дроби и умножим обе части уравнения на 20:

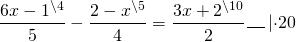
Можно, конечно, сразу же умножить дополнительный множитель на числитель каждой дроби.

Скобки — друзья ученика :). Поэтому лучше воспользоваться их помощью:

Особенно полезны скобки в случае, когда перед дробью стоит знак «минус».

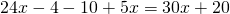
Но, к сожалению, наибольшее количество ошибок при решении линейных уравнений с дробями допускается именно на этом шаге.

После раскрытия скобок можно сразу же перенести неизвестные в одну сторону уравнения, известные — в другую

Линейные уравнения.

Решение линейных уравнений. Правило переноса слагаемого.

Правило переноса слагаемого. При решении и преобразовании уравнений зачастую возникает необходимость переноса слагаемого на другую сторону уравнения. Заметим, что слагаемое может иметь как знак «плюс», так и знак «минус».

Согласно правилу, перенося слагаемое в другую часть уравнения, нужно изменить знак на противоположный.

Кроме того, правило работает и для неравенств. Примеры переноса слагаемого: 5x+2=7x−6.

Сначала переносим 5x из левой части уравнения в правую: 2=7x−6−5x. Далее переносим (−6) из правой части в левую: 2+6=7x−5x. Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+».

При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение. −3×2(2+7x)−4+y=0. Переносим 1-е слагаемое в правую сторону уравнения. Получаем: −4+y=3×2(2+7x). Обратите внимание, что в нашем примере слагаемое — это выражение (−3×2(2+7x)).

Поэтому нельзя отдельно переносить (−3×2) и (2+7x), так как это составляющие слагаемого. Именно поэтому не переносят (−3×2⋅2) и (7x).

Однако мы модем раскрыть скобки и получить 2 слагаемых: (−3x‑⋅2) и (−3×2⋅7x). Эти 2 слагаемых можно переносить отдельно друг от друга. Таким же образом преобразовывают неравенства: 7x+25>14 Собираем каждое число с одной стороны.

Получаем: 7x>14−25 или 7x>−11 Доказательство. 2-е части уравнения по определению одинаковы, поэтому можем вычитать из обеих частей уравнения одинаковые выражения, и равенство будет оставаться верным. Вычитать нужно выражение, которое в итоге нужно перенести в другую сторону.

Тогда по одну сторону знака «=» оно сократится с тем, что было.

А по другую сторону равенства выражение, которое мы вычли, появится со знаком «-». Это правило зачастую используется для решения . Для решения используются другие методы.

Решение уравнений

Обычно в таком случае говорят, что обе части уравнения разделили на 5.

Второе уравнение: То же самое мы бы получили, если бы воспользовались правилом отыскания неизвестного множителя. Сделаем вывод: Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число. Третье уравнение: Это уравнение можно переписать так: Следующее уравнение:

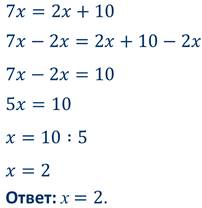
Сделаем вывод: Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

И решим ещё одно уравнение: Чтобы решить уравнение, содержащее подобные слагаемые нужно: 1) слагаемые, содержащие переменную, перенести в левую часть уравнения, а числа – в его правую часть, не забывая при переносе менять знаки на противоположные; 2) привести

Как решать дробные уравнения?

Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем – настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись. Итак, вперёд! Что такое дробное уравнение? Примеры. Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби.

Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном. Например, вот такое уравнение:

Или такое:

Или вот такое:

И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся.

Либо это линейные уравнения, либо квадратные.

Решение уравнений с переменной в знаменателе дроби

Вспомним , что для этого необходимо умножить первое слагаемое первого умножить на каждое слагаемое второго многочлена, затем второе слагаемое первого многочлена умножить на каждое слагаемое второго многочлена и результаты сложить \[\left(2x+3\right)\left(х+3\right)=2х\cdot х+2х\cdot 3+3\cdot х+3\cdot 3={2х}^2+6х+3х+9\] Приведем подобные слагаемые в полученном выражении \[\left(2x+3\right)\left(х+3\right)=2х\cdot х+2х\cdot 3+3\cdot х+3\cdot 3={2х}^2+6х+3х+9=\] \[{=2х}^2+9х+9\] Выполним аналогично преобразование в числителе второй дроби-произведем умножение многочленов $\left(x-5\right)\left(2х-1\right)=х\cdot 2х-х\cdot 1-5\cdot 2х+5\cdot 1={2х}^2-х-10х+5={2х}^2-11х+5$ Тогда уравнение примет вид: \[\frac{{2х}^2+9х+9}{(2x-1)(х+3)}-\frac{{2х}^2-11х+5}{(x+3)(2х-1)}=0\] Теперь дроби с одинаковым знаменателем, значит можно производить вычитание.